Тема:  Узагальнення і систематизація знань з теми “ Вступ до стереометрії ”. Побудова перерізів куба, піраміди.
Підготовка до контрольної роботи

Вчитель: Сороколіта І.М.

Мета:

• повторити геометричні поняття й твердження, продовжити формувати  в учнів розуміння поняття перерізу, більш детальніше розглянути метод слідів, навчити будувати більш складні перерізи, показати значення стереометрії в житті людини;
• розвивати логічне мислення , просторову уяву, увагу, пам'ять та вміння вибудовувати своє пояснення,розвивати дизайнерські уміння та навички, розвивати творчий потенціал учнів;
• виховати відповідальне ставлення до роботи, дисциплінованість, самостійність, взаємодопомогу та взаємопідтримку, виховувати інтерес до технічних знань. 

Тип уроку: комбінований.

Обладнання: план-конспект, презентація, друковані матеріали, моделі геометричних фігур.

Методи:

• словесні: розповідь, бесіда, самооцінка, взаємонавчання, методи мотивації, збудження інтересу, гра «Не розірви ланцюг»;;
• наочні: робота з роздатковим матеріалом ;
• практичні: розв'язування вправ, самостійна робота, робота в групах, метод повторення, поступового ускладнення завдань.

І. Організаційни момент

Психологічне налаштування учнів на урок

Очікування від уроку

ІІ. Мотивація  уроку

Для чого це потрібно? 

Підготовка до контрольної роботи

 “Коли добре щось умієте – того не забувайте, а чого не вмієте – того учітесь…” В.Мономах

ІІІ.Актуалізація знань 

1) Опорний конспект до уроку для учнів

Вступ до стереометрії

Стереометрія - розділ геометрії, що вивчає фігури в просторі

Основні фігури в просторі: точка, пряма , площина

Аксіоми стереометрії:

Аксіома 1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй

Аксіома 2. Якщо дві різні прямі мають спільну точку, то через них можна провести площину і до того ж тільки одну

Аксіома 3. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку

Наслідки з аксіом стереометрії:

1)                Через три точки, що не лежать на одній прямій можна провести площину і до того ж тільки одну;

2)                Через пряму і точку, що не належить їй, можна провести площину і до того ж тільки одну;

3)                Якщо дві точки прямої на лежать площині, то і вся пряма належить цій площині.

Перерізи

• Якщо принаймні дві точки просторової фігури лежать по різні боки від площини, то говорять, що площина цю фігуру перетинає. А площину називають січною.
• Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини
• Вид перерізу залежить від розміщення площини
• кількість сторін многокутника перерізу не може перевищувати кількості граней даного многогранника

Площину перерізу можна задати:

1. Трьома точками, що не лежать на одній прямій;

2. Прямою і точкою, що не лежить на ній;

3. Двома прямими, що перетинаються;

4. Двома паралельними прямими;

                     Побудувати переріз многогранника площиною – означає:

ü     в площині кожної перетнутої грані вказати дві точки, що належать перерізу;

ü     з'єднати ці точки прямою;

ü     знайти точки перетину прямої з ребрами многогранника.

                                           Метод слідів:

Якщо площина α перетинає площину β по прямій а, то пряму а називають слідом площини α на площину β.

Метод слідів включає три важливих пункти:

v  Будується лінія перетину (слід) січної площини з площиною основи многогранника.

v  знаходимо точки перетину січної площини з ребром многогранника.

v  Будуємо і заштриховуємо переріз.

 

 2) Гра "Не розірви ланцюг" (або математичне лото)

Що таке стереометрія?	Многокутник , у якого кількість сторін не перевищує кількість граней многогранника
Стереометрія - розділ геометрії, що вивчає фігури в просторі	Які фігури є основними в просторі?
Основні фігури в просторі: точка, пряма , площина	Сформулюй аксіому про належність точок площині
Аксіома 1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй	Сформулюй аксіому про єдність площини
Аксіома 2. Якщо дві різні прямі мають спільну точку, то через них можна провести площину і до того ж тільки одну	Сформулюй аксіому про перетин площин
Аксіома 3. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку	Як можна задати площину?
— Трьома точками, які не   лежать на одній прямій. — Прямою і точкою, яка   не лежить на ній. — Двома прямими, що перетинаються.	Яку площину називають січною?
Якщо принаймні дві точки просторової фігури лежать по різні боки від площини, то говорять, що площина цю фігуру перетинає. А площину називають січною.	Що називають перерізом многогранника?
Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини	Яка може бути кількість сторін у многокутника перерізу?
кількість сторін многокутника перерізу не може перевищувати кількості граней даного многогранника	Що означає побудувати переріз многогранника?
ü   в площині кожної перетнутої грані вказати дві точки, що належать перерізу; ü    з'єднати ці точки прямою; ü    знайти точки перетину прямої з ребрами многогранника.	Що таке слід площини?
Якщо площина α перетинає площину β по прямій а, то пряму а називають слідом площини α на площину β.	В чому полягає метод слідів?
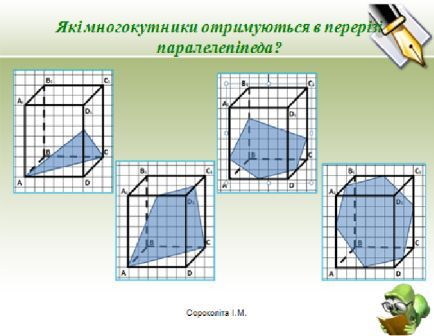
vБудується лінія перетину (слід) січної площини з площиною основи многогранника. v знаходимо точки перетину січної площини з ребром многогранника. v Будуємо і заштриховуємо переріз.	Який многокутник може утворюватись в перерізі многогранника?

 3) Дати відповіді на запитання

 1.Яке мінімальне число точок визначає пряму в просторі?

4.Скільки площин можна провести через пряму і точку?

5. Як розміщені пряма а і точка А , якщо через них сможна провести дві різних площини?

6. Пять точок не лежать в одній площині. Яке найбільше число цих точок може лежати на одній прямій?

7. Скільки площин можна провести через точки А, В і С, якщо АВ=5, ВС=3, АС=4?

8.Чи можна через точку перетину діагоналей паралелограма провести пряму, що не перетинає його сторони?

9. Центр кола і дві точки, що є кінцями діаметра, лежать в одній площині. Чи лежать в одній площині всі точки кола?

  

ІV.Розвязування задач 

   

 

 

 

 

 

 

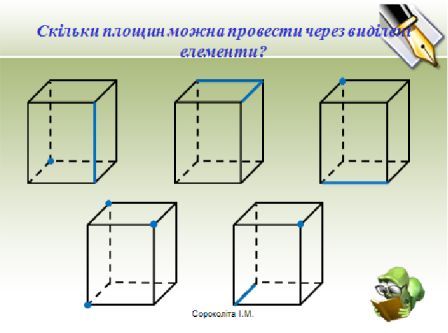
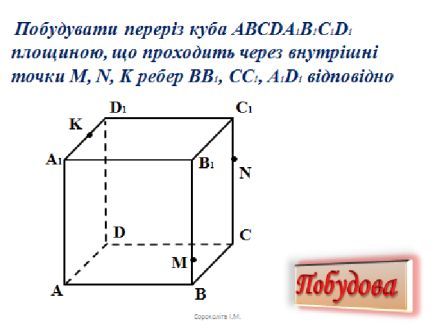
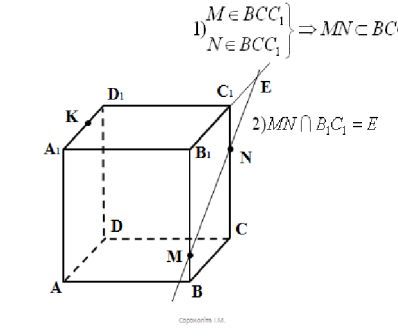
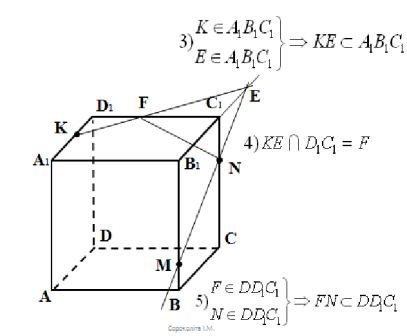
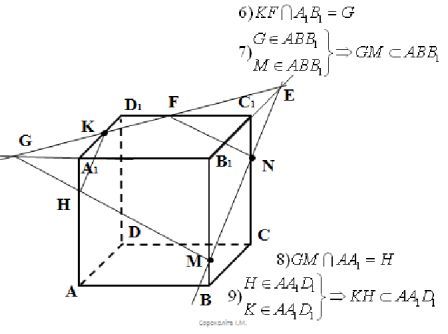
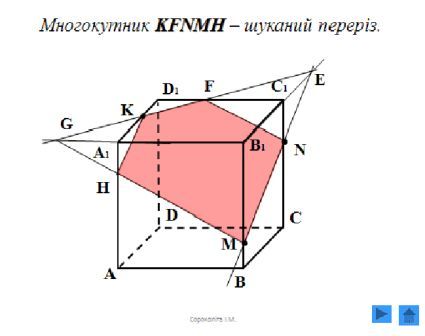
V.Самостійна робота 

Побудувати переріз через вказані точки

 

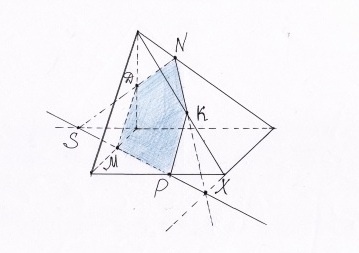
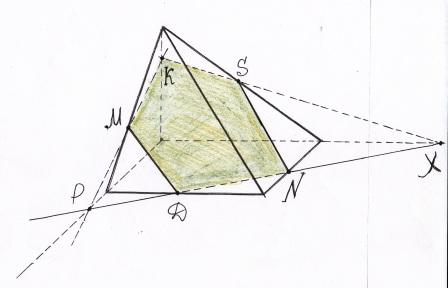
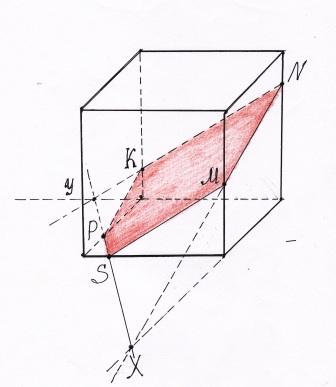
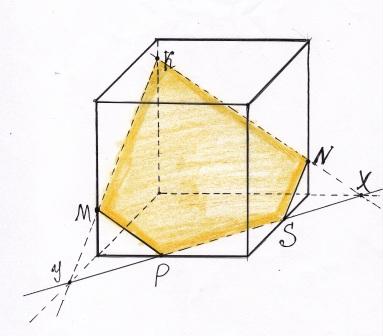
 Розвязування задач прикладного характеру

№1

Столяр перевіряє, чи лежать кінці ніжок стільця в одній площині, прикріпивши до кінців ніжок навхрест дві нитки. На чому ґрунтується така перевірка?

№2
Штативи для багатьох інструментів (фотоапарата, геодезичних приладів – нівеліра, теодоліта та ін..) виготовляють у вигляді триноги. Чому підставка з такою кількістю ніг є стійкою?

№3
Тесля виявляє недоліки в обробці деревяного бруска або дошки дивлячись уздовж обробленої поверхні. На чому ґрунтується така перевірка?

№4
Чому мотоцикл із коляскою стоїть на дорозі стійко, скутеру без коляски потрібна додаткова опора?  

№5
Чому незамкнені двері відчиняються, а замкнені – нерухомі?

№6
Чому стілець із трьома ніжками, розміщеними по колу, завжди стоїть на підлозі стійко, а з чотирма незавжди?  

Картка самооцінювання для учнів 

 

Прізвище_______________

Листок самооцінювання учня

Постав собі від 0 до 2 балів, якщо ти:

відповів правильно на тестове запитання____

склав правильно математичне  лото____

відповідав на питання вчителя____

побудував правильно переріз_____

розв’язав прикладну задачу____

виконав індивідуальне завдання __

підготував цікаву інформацію до уроку______

мені було цікаво на уроці____

Сума балів (оцінка)______

Домашнє завдання:
підготуватися до контрольної роботи, повторити §3,4,5,
виконати на сторінці 63 типові завдання для контрольної роботи
(підручник Геометрія,10
профільний рівень, авт.Бевз)