Припустимо, що у просторі є точка O. Нехай ця точка буде початком двовимірної системи координат з осями x та y, та тривимірної з осями u, v, w. Нехай γ – площина, у якій лежить система координат xOy.

Нехай кут між векторами   та     -  α, a кут між векторами  та   - β.

Не важко довести, що координати проекцій на площину γ одиничних векторів осей тривимірної системи координат у системі координат xOy будуть:

 

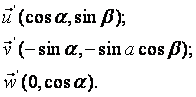
Очевидно, координати проекції точки  будуть рівні координатам радіус-вектора .

 

 

Спробуємо створити динамічний рисунок у програмі GeoGebra, у якому будуть відображатись проекції одиничних векторів тривимірної системи координат.

Виконаємо таку послідовність дій.

1. Для початку потрібно додати кути α і β, які можна буде динамічно міняти.

  Додаємо повзунки α і β (не забуваємо вказати, що це кут).

 

1. Тепер нам потрібно зобразити проекції векторів .

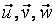 Найзручніше це зробити за допомогою командного рядка, ввівши у неї команди:

u = (cos(β), -sin(α) sin(β))

v = (-sin(β), -sin(α) cos(β))

w = (0, cos(α))

Після цього на екрані з’являться три вектори. При зміні значень кутів α і β, вони повинні обертатися.

 

Але існує більш зручний спосіб зміни кутів α і β, ніж використання повзунків. Метод полягає в тому, щоб замість повзунків використовувати точку.

Виконаємо таку послідовність дій:

1.   Поставимо точку A.
2. Введемо послідовно команди

xa = x(A)

ya = y(A)

Таким чином, ми ввели два числа: xa та ya – координати абсциси та ординати точки A відповідно.

1. Тепер команди для задання векторів трохи зміняться:

u = (cos(xa), -sin(ya) sin(xa))

v = (-sin(xa), -sin(ya) cos(xa))

w = (0, cos(ya))

У такому випадку, для того, щоб змінювати кути α і β,  потрібно пересувати точку A.

 

Далі спробуємо створити динамічну модель куба   з довжиною ребра a.

1. Будуємо вектори  одним з вище описаних способів.

2.  Ставимо повзунок a, виставляємо межі числа від 0.1 до 20.

3. Припускаємо, що початок тривимірної системи координат лежить на перетині двох діагоналей куба. В такому випадку координати точок будуть такі:

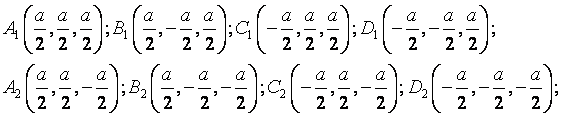 4. Найзручніше вводити координати в таблиці (Ctrl+Shift+S).

У комірці A1 введемо «a/2», програма автоматично обрахує значення.

Заповнимо таблицю координатами з пункту 2. Координати точки  у такому випадку будуть розташовані у комірках A1, B1 та C1.

 

 

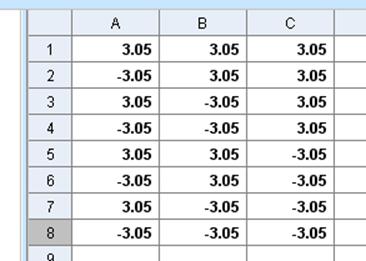
5. Тепер по цих координатах потрібно побудувати проекції точок.

 Для початку добавимо точку W (вона нам знадобиться для того, щоб отриману проекцію фігури можна було пересувати по екрану).

6. Виберемо з меню пункт Опції\Позначення\Нові об’єкти відсутні. Після чого усі нові точки, що з’являтимуться на екрані будуть з’являтись без позначень.

7. Далі у комірку D1 введемо: W + A1 u + B1 v + C1 w. Після чого з’явиться перша вершина куба, а у комірці будуть записані координати точки.

8. Вводити W + A2 u + B2 v + C2 w у комірці D2 не обов’язково.

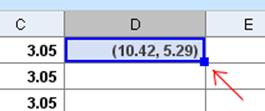 Достатньо  потягнути за квадратик у кутку виділеної комірки D1 до комірки D8 включно. Комірки D2-D8 заповняться автоматично.

1.   9.  Тепер усі вершини зображені на рисунку. 

   Далі достатньо з’єднати їх відрізками у потрібному порядку.

10.У властивостях кожної вершини можна вказати її назву в полі «Надпис», а у меню «Показувати позначення» вибрати пункт «Заголовок».

 

Таким чином ми отримали тривимірну модель куба.  Але, при побудові рисунка до стереометричних задач важливим є зображення невидимих ліній пунктиром. Це проблематично, оскільки при різних значеннях кутів α та β невидимою може виявитись будь-яка з зображених ліній.

Тому, пропонується створити інструмент для  програми GeoGebra, який в залежності від кутів α і β та положення прямої визначатиме видима вона чи ні, і зображатиме її суцільною або пунктирною відповідно.

 

Потрібно зауважити, що для визначення кута у програмі GeoGebra важливим є порядок запису вершин. Тобто . Напрям усіх кутів - проти годинникової стрілки.

 

Нехай маємо тетраедр ABCD. Розглянемо умови видимості ребра AB.

  

 

  

       

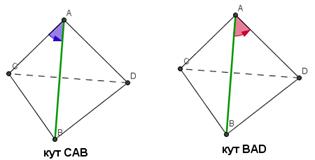
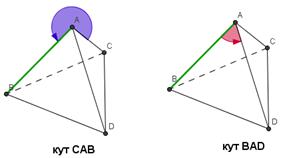
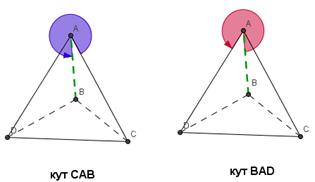
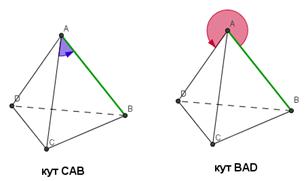
 Якщо один з кутів CAB або BAD менший  180º, то відрізок AB видно і його потрібно зображати суцільною лінією. У іншому ж випадку – пунктирною. Цю умову можна використати для будь-якої піраміди або призми, в основі якої випуклий чотирикутник, умовно підібравши для потрібного відрізка тетраедр, вершинами якого будуть деякі вершини даної фігури.

Щоразу вводити у програмі таку об’ємну умову незручно. Тому варто створити інструмент, який частину роботи виконуватиме автоматично.

Для цього виконаємо таку послідовність дій:

1. Відкриємо нове вікно програми GeoGebra.

2. Приберемо осі (Вид\Оси) та відобразимо сітку (Вид\Сетка).

3.   Поставимо нові точки  A,B,C,D так, як показано на рисунку.



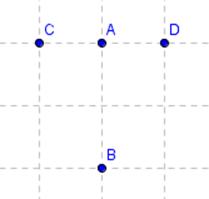
4. Впишемо команди в командний рядок:

Якщо[Кут[C,A,B]Кут[B,A,D], Відрізок [A,B]]

Якщо[¬(Кут[C,A,B]Кут[B,A,D], Відрізок [A,B]]

Тепер викличемо вікно властивостей відрізка b і у вкладці “Стиль” у пункті “Стиль линии” виберемо пунктирну лінію. Після цього, якщо поміняти точки C і D місцями, то відрізок AB повинен стати пунктирним.

5. Викличемо вікно Инструменты\Создать новый инструмент. Як вихідні об’єкти виберемо відрізки a і b. Як вхідні – точки A, B, C, D (у такому ж порядку).

У вкладці “Имя и значок” у полі “Имя” введемо “Відрізок 3D”. Поле “Команда” заповниться автоматично.

   Значок можна створити самому або завантажити за адресою http://mathforum.at.ua/3d.jpg.

6. Викличемо вікно Инструменты\Управление инструментами. Натиснемо “Сохранить как” і збережемо інструмент під назвою “Відрізок3D.ggt”]

 

Після виконання описаних вище дій створиться файл формату .ggt з інформацією про інструмент, який ми будемо використовувати для подальшого створення об’ємних динамічних ілюстрацій.

 

Створимо тепер шаблон для подальшої роботи з векторами та щойно створеним інструментом.

1. Збережемо файл як “Шаблон.ggb”.

2. Приберемо осі.

3.  Поставимо точку і задамо їй назву Obert.

4. Введемо послідовно команди

xa = x(Obert)

ya = y(Obert)

u = (cos(xa), -sin(ya) sin(xa))

v = (-sin(xa), -sin(ya) cos(xa))

w = (0, cos(ya))

5. Виділимо отримані вектори і у властивостях вкажемо їх не відображати.

6. Відкриємо файл з інструментом “Відрізок3D”.

7. Натиснемо за “Сохранить”.

 

Тепер спробуємо побудувати модель куба, використовуючи щойно створений шаблон.

1. Відкриємо файл “Шаблон.ggb” та збережемо його як “Куб.ggb”.

2. Повторюємо дії з пунктів 2-8 попередньої побудови куба.

3. Тепер потрібно зобразити ребра. Використаємо створений нами інструмент “Відрізок.ggt”.

 Натискаємо на іконку і вибираємо точки у такій послідовності: D₅, D₁, D₇, D₆. Після цього повинно з’явитися ребро D₁D₅.

Далі послідовно використовуючи інструментом “Відрізок3D”, вибираємо по 4 точки, додаючи до ілюстрації по новому ребру. Вибираємо точки у такій послідовності:

D₇, D₃, D₈, D₅;   D₈, D₄, D₆, D₇;   D₆, D₂, D₅, D₈;   D₈, D₆, D₅, D₄;

D₆, D₅, D₇, D₂;   D₅, D₇, D₈, D₁;   D₇, D₈, D₆, D₃;   D₃, D₁, D₂, D₇;

D₁, D₂, D₄, D₅;   D₂, D₄, D₃, D₆;   D₄, D₃, D₁, D₈;

Отримали куб. При його обертанні видимі ребра зображаються суцільними відрізками, а невидимі – пунктирними.

4. У властивостях точок D1-D8 в пункті “Показывать обозначения” вказуємо “Заголовок”. В пункті “Надпись” для кожної точки вказуємо її назву.